Asymptotic distributions

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import seaborn as sns
import scikits.bootstrap as boot

The canonical case

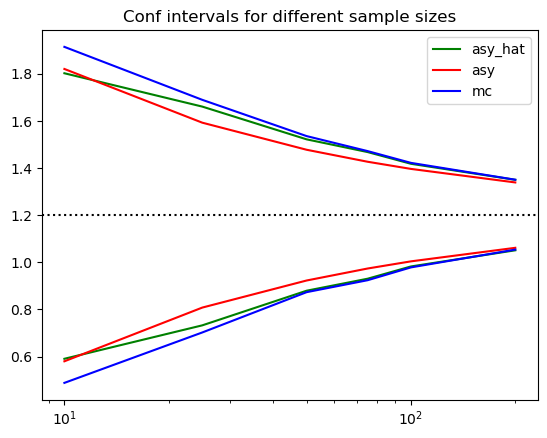
We simulate a linear model with normal errors, we compare the finite sample distribution to the asymptotic distribution.

def ols_normal(beta,X,N,e_sd):
    """ Simulates the errors, estimates OLS coefficient, se, tstat and CI"""
    E = e_sd*np.random.normal(size=N)
    Y = beta*X[0:N] + E
    cov = np.cov(Y,X[0:N])
    beta_hat = cov[0,1]/cov[1,1]
    beta_se  = (Y-beta_hat*X[0:N]).std()/(np.sqrt(N)*X[0:N].std())    
    tstats_asy = (beta_hat-beta)/beta_se    
    ci_asy = beta_hat + beta_se * np.array([-1.96,1.96])
    return({
        'beta':beta_hat,
        'se':beta_se,
        'tstats_asy':tstats_asy,
        'ci_lb':ci_asy[0],
        'ci_ub':ci_asy[1], 
        'N':N})

beta = 1.2
R = 10000
e_sd = 1.0

X = np.random.normal(size=200)
res = [ols_normal(beta,X,N,e_sd) for _ in range(R) for N in [10,25,50,75,100,200]]
sim = pd.DataFrame(res)

# append theoretical asymptotic CI 
sim['ci_lb_asy'] = beta - e_sd*1.96/np.sqrt(sim['N'])
sim['ci_ub_asy'] = beta + e_sd*1.96/np.sqrt(sim['N'])

sim_tmp = sim.groupby('N').mean()
sim_tmp['ub'] = sim.groupby('N')['beta'].quantile(0.975)
sim_tmp['lb'] = sim.groupby('N')['beta'].quantile(0.025)
sim_tmp = sim_tmp.reset_index()

plt.plot(sim_tmp['N'],sim_tmp['ci_lb'], color="green", label="asy_hat")
plt.plot(sim_tmp['N'],sim_tmp['ci_lb_asy'], color="red", label="asy")
plt.plot(sim_tmp['N'],sim_tmp['lb'], color="blue", label="mc")

plt.plot(sim_tmp['N'],sim_tmp['ci_ub'], color="green")
plt.plot(sim_tmp['N'],sim_tmp['ci_ub_asy'], color="red")
plt.plot(sim_tmp['N'],sim_tmp['ub'], color="blue")

plt.axhline(beta,linestyle=":",color="black")
plt.legend()
plt.title("Conf intervals for different sample sizes")

plt.xscale('log')
plt.show()

png

Change the error distribution to Pareto

from scipy.stats import pareto

def ols_pareto(beta,X,N,alpha):
    """ Simulates the errors, estimates OLS coefficient, se, tstat and CI"""
    E = np.random.pareto(alpha, N) # !!! new distribution here
    Y = beta*X[0:N] + E
    cov = np.cov(Y,X[0:N])
    beta_hat = cov[0,1]/cov[1,1]
    beta_se  = (Y-beta_hat*X[0:N]).std()/(np.sqrt(N)*X[0:N].std())    
    tstats_asy = (beta_hat-beta)/beta_se    
    ci_asy = beta_hat + beta_se * np.array([-1.96,1.96])
    return({'beta':beta_hat,'se':beta_se,'tstats_asy':tstats_asy,'ci_lb':ci_asy[0],'ci_ub':ci_asy[1],'N':N})

beta = 0.5
R = 10000
alpha = 3.0 # Pareto parameter

e_sd = np.sqrt(pareto.stats(alpha, moments='v'))

X = 0.2*np.random.normal(size=200)
res = [ols_pareto(beta,X,N,alpha) for _ in range(R) for N in [10,25,50,75,100,200]]
sim = pd.DataFrame(res)

sim['ci_lb_asy'] = beta - e_sd*1.96/np.sqrt(sim['N'])
sim['ci_ub_asy'] = beta + e_sd*1.96/np.sqrt(sim['N'])

sim_tmp = sim.groupby('N').mean()
sim_tmp['ub'] = sim.groupby('N')['beta'].quantile(0.975)
sim_tmp['lb'] = sim.groupby('N')['beta'].quantile(0.025)
sim_tmp = sim_tmp.reset_index()

plt.plot(sim_tmp['N'],sim_tmp['ci_lb'], color="green", label="asy_hat")
plt.plot(sim_tmp['N'],sim_tmp['ci_lb_asy'], color="red", label="asy")
plt.plot(sim_tmp['N'],sim_tmp['lb'], color="blue", label="mc")

plt.plot(sim_tmp['N'],sim_tmp['ci_ub'], color="green")
plt.plot(sim_tmp['N'],sim_tmp['ci_ub_asy'], color="red")
plt.plot(sim_tmp['N'],sim_tmp['ub'], color="blue")

plt.axhline(beta,linestyle=":",color="black")
plt.legend()
plt.title("Conf intervals for different sample sizes")

plt.xscale('log')
plt.show()

# fixme maybe an error in the red
# finite sample distribution based on normal assumption

png

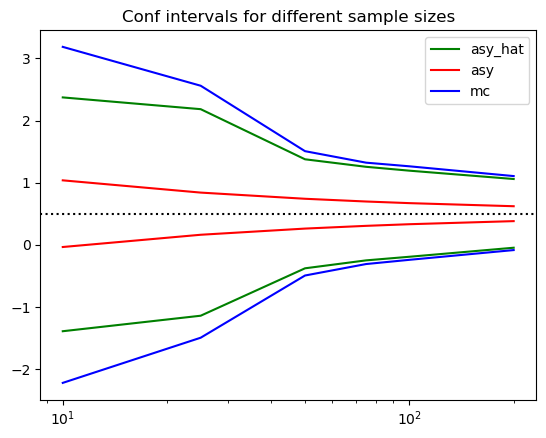
We plotted 3 objects. The blue line is directly the $(p,1-p)$ quantiles of the distribution of generated estimates. We can think of this as the true finite sample distribution for this particular draw of $X$ . The red line is the asymptotic confidence interval that uses the true variance of $X$ and the error term. Finally the green line is the average over confidence intervals across replciations generated using the asymptotic normality assumption and the sample variance of the residual.

Delta method and C.I.

Let's now look at the square of $\beta$ . From the delta method we have that

$\sqrt{n} ( \beta_n^2 - \beta^2 ) \rightarrow \mathcal{N} \Big(0, \frac{\sigma_e^2}{\sigma_x^2} 4\beta^2 \Big)$

np.random.seed(10)
beta = 0.5
N = 50
R = 2000
X = np.random.normal(size=N)

# we want to compare MC CI to realized CI

ci_asy = np.zeros((R,2))
beta2_mc = np.zeros((R)) # we store the MC realizations 

for i in range(R):
    E = np.random.normal(size=N)
    Y = beta*X + E

    cov = np.cov(Y,X)
    beta_hat = cov[0,1]/cov[1,1]    
    beta_se  = (Y-beta_hat*X).std()/(np.sqrt(N)*X.std())

    ## we construct the estimate and the CI using the delta method
    beta2_mc[i] = beta_hat ** 2
    beta2_se = beta_se * 2 * np.abs(beta_hat) # see delta method formula
    ci_asy[i,:] = beta_hat ** 2 + beta2_se * np.array([-1.96,1.96])

plt.subplot(1,2,1)
plt.hist(ci_asy[:,0],alpha=0.3,label="mc asy CI",color="blue",density=True)
plt.axvline( ci_asy[:,0].mean(),color="blue" ,label="mc asy CI (mean)")
plt.axvline( np.quantile(beta2_mc,0.025) ,color="red" ,label="mc CI")
plt.title("lower bound CI 0.025")
plt.legend()

plt.subplot(1,2,2)
plt.hist(ci_asy[:,1],alpha=0.3,label="mc asy CI",color="blue",density=True)
plt.axvline( ci_asy[:,1].mean(),color="blue",label="mc asy CI (mean)" )
plt.axvline( np.quantile(beta2_mc,0.975) ,color="red",label="mc CI" )
plt.legend()
plt.title("upper bound CI 0.975")
plt.show()

png

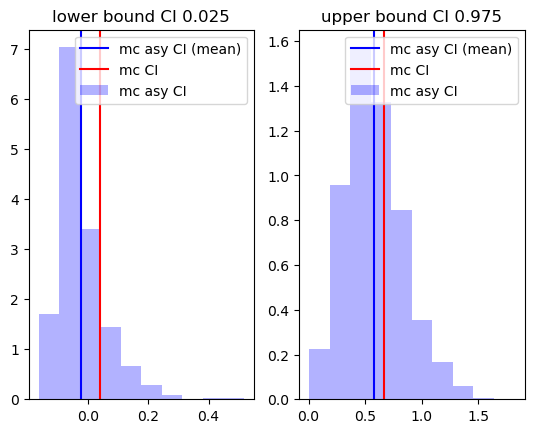
In particular, we note that while the Monte-Carlo CI does not include 0, and hence 0 should be rejected, the asymptotic confidence interval includes 0. In this case the asymptotic CI appears to be on average to the right of the true monte-carlo distribution across replications.

Bootstrap distribution

We create the resampling distribution and compare it to the finite sample distribution

def bootstrap_CI(Y,X,B=500):
    """ Computes the CI at 0.05 percent for the OLS estimate """
    N = len(Y)
    beta_dm_vec_bs = np.zeros((B))
    tstat_bs = np.zeros((B))

    # compute the OLS estimate in the sample
    cov = np.cov(Y,X)
    beta_hat =  cov[0,1]/cov[1,1]
    beta_se_r0  = (Y-beta_hat*X).std()/(np.sqrt(N)*X.std())    
    beta2_se_r0 = beta_se_r0 * 2 * np.abs(beta_hat)

    # bootstrap
    for i in range(B):
        I = np.random.randint(N,size=N)
        Ys = Y[I]
        Xs = X[I]
        cov = np.cov(Ys,Xs)
        beta_hat_r = cov[0,1]/cov[1,1]     # OLS estimate for each replication
        beta_dm_vec_bs[i] = beta_hat_r**2  # transformed estimate for each replciation

        beta_se_r  = (Ys-beta_hat_r*Xs).std()/(np.sqrt(N)*Xs.std())    
        beta2_se_r = beta_se_r * 2 * np.abs(beta_hat_r)
        tstat_bs[i] = beta_hat_r**2 / beta2_se_r

    # compute bias is any
    M = np.mean(beta_dm_vec_bs)
    bias = M - beta_hat**2

    U = np.quantile(beta_dm_vec_bs,0.975)-bias
    L = np.quantile(beta_dm_vec_bs,0.025)-bias        
#     U = np.quantile(beta_inv_vec_bs,0.975)
#     L = np.quantile(beta_inv_vec_bs,0.025)

    return(M,L,U)

np.random.seed(10)
import tqdm

all = []
for N in [50]:

    R = 500 # number of replications
    B = 500 # number of boostraps
    X = np.random.normal(size=N)

    # construct the null distribution
    ci_bs = np.zeros((R,2))
    ci_asy = np.zeros((R,2))
    beta2_mc = np.zeros((R))
    beta2_bs = np.zeros((R))

    for i in tqdm.tqdm(range(R)):
        E = np.random.normal(size=N)
        Y = beta*X + E
        cov = np.cov(Y,X)
        beta_hat = cov[0,1]/cov[1,1]
        beta2_mc[i] = beta_hat**2    # transformed estimate

        beta_se  = (Y-beta_hat*X).std()/(np.sqrt(N)*X.std())    
        beta2_se = beta_se * 2 * np.abs(beta_hat)

        # asymptotic confidence interval using delta method
        ci_asy[i,:] = beta_hat**2 + beta2_se * np.array([-1.96,1.96])

        # bootstrap estimates
        beta2_bs[i], ci_bs[i,0], ci_bs[i,1] = bootstrap_CI(Y,X,B)

100%|██████████| 500/500 [00:22<00:00, 22.47it/s]

plt.subplot(1,2,1)
plt.hist(ci_asy[:,0],alpha=0.3,color="blue",density=True)
plt.axvline( ci_asy[:,0].mean(),color="blue" , label="asy")
plt.axvline( np.quantile(beta2_mc,0.025) ,color="red" , label="mc CI")
plt.title("asymptotic CI 0.025")
plt.legend()

plt.subplot(1,2,2)
plt.hist(ci_asy[:,1],alpha=0.3,color="blue",density=True)
plt.axvline( ci_asy[:,1].mean(),color="blue" , label="asy")
plt.axvline( np.quantile(beta2_mc,0.975) ,color="red", label="mc CI" )
plt.title("asymptotic CI 0.975")
plt.legend()

plt.show()

png

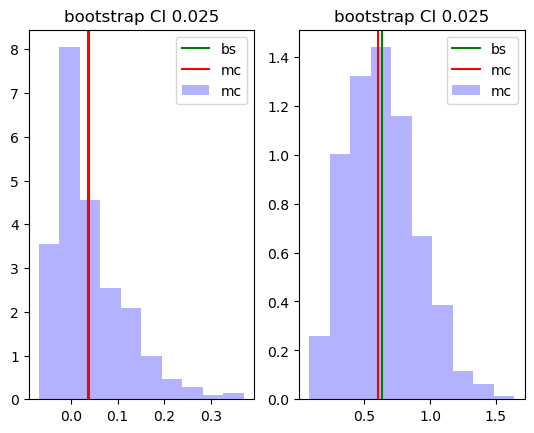
plt.subplot(1,2,1)
plt.hist(ci_bs[:,0],alpha=0.3,label="mc",color="blue",density=True)
plt.axvline( ci_bs[:,0].mean(),color="green" , label="bs")
plt.axvline( np.quantile(beta2_mc,0.025) ,color="red" , label="mc")
plt.title("bootstrap CI 0.025")
plt.legend()

plt.subplot(1,2,2)
plt.hist(ci_bs[:,1],alpha=0.3,label="mc",color="blue",density=True)
plt.axvline( ci_bs[:,1].mean(),color="green", label="bs" )
plt.axvline( np.quantile(beta2_mc,0.975) ,color="red" , label="mc")
plt.title("bootstrap CI 0.025")
plt.legend()

plt.show()

png

# Boostrap CI on average
ci_bs.mean(0)

array([0.03916983, 0.63744695])

# Asy CI on average
ci_asy.mean(0)

array([-0.0254555 ,  0.56548982])

# 
np.quantile(beta2_mc,[0.025,0.975])

array([0.03712143, 0.60464131])

Biased in the estimate itself

We compare $\beta$ to $\beta_n$ to $\beta^*_n$ . We notice for instance that $\beta < \beta_n <\beta^*_n$

beta**2

0.25

beta2_mc.mean()

0.2700171565383394

beta2_bs.mean()

0.29472310724131867

2*beta2_mc.mean() - beta2_bs.mean()

0.24531120583536015

plt.subplot(1,2,1)
plt.hist( beta2_mc ,alpha=0.3,label="mc",color="blue",density=True)
plt.axvline( beta2_mc.mean(),color="blue" )
plt.axvline( beta**2 ,color="red" )
plt.title("OLS MC")

plt.subplot(1,2,2)
plt.hist( 2*beta2_mc - beta2_bs ,alpha=0.3,label="mc",color="blue",density=True)
plt.axvline( (2*beta2_mc - beta2_bs).mean(),color="blue" )
plt.axvline( beta**2 ,color="red" )
plt.title("Bootstrap corrected MC")

plt.show()

png

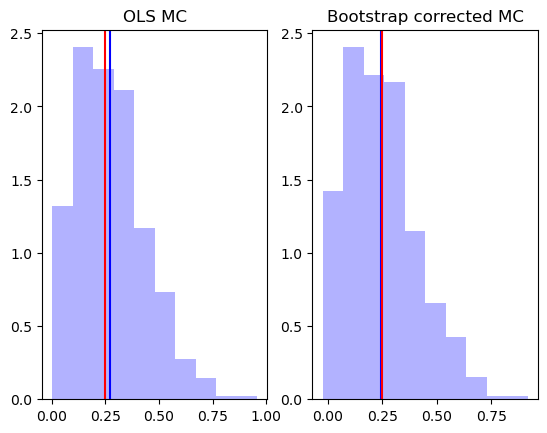
A simpler exercise - Variance

Let's look at the variance estimator:

$s^2_n = \frac{1}{n} \sum_i ( X_i - \bar{X} ) ^2$

This is an consistent estimator, however we know from stat class that it is biased at finite $n$ . We are going to look at the construction of confidence intervals based on asymptotic properties as well as bootstrap.

link to source code for bootstrap code bootstrap

From the central limit theorem, we have in particular that:

$\sqrt{n}( s^2_n - \sigma^2 ) \rightarrow_d N(0, \mu_4 - \sigma^4 )$

where $\mu_4 = E[ (X_i - \mu)^4]$ .

def var_stat(X,weights=None,bias=0):
    Xbar = X.mean() 
    Var  = ( (X-Xbar)**2 ).mean() 
    return(Var + bias/len(X))

def F_normal(N, bs=True, bias=0):
    X = np.random.normal(size=N)
    varn = var_stat(X,bias=bias)

    # compute asymptotic standard errors
    mu  = X.mean()
    s2  = ( (X-mu)**2 ).mean() 
    mu4 = ( (X-mu)**4 ).mean() 

    ci_asy_lb = varn - 1.96*np.sqrt( (mu4 - s2**2)/N)
    ci_asy_ub = varn + 1.96*np.sqrt( (mu4 - s2**2)/N)

    return({'theta':varn, 
            'ci_asy_lb': ci_asy_lb,
            'ci_asy_ub': ci_asy_ub,
            'N':N})

# we generate the finite sample distribution
res = [F_normal(N,False,bias=0) for N in [10,20,30,50,100,200,500,2000] for _ in range(5000)]
res = pd.DataFrame(res)

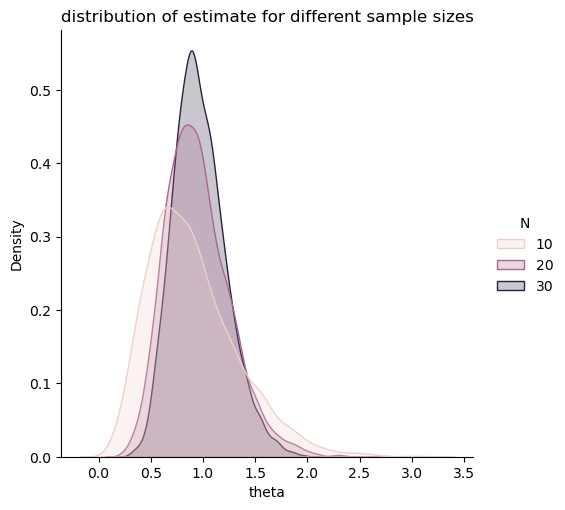
sns.displot(res.query('N<50'),x='theta',hue='N', kind="kde", fill=True)
plt.title("distribution of estimate for different sample sizes")
plt.show()

png

res_sum = res.groupby('N').mean()
# res_sum['lb'] = res.groupby('N')['theta'].quantile(0.025)
# res_sum['ub'] = res.groupby('N')['theta'].quantile(0.975)
res_sum['sd'] = res.groupby('N')['theta'].std()
res_sum['cov_asy'] = res.eval('c = (ci_asy_lb < 1) &  (ci_asy_ub > 1) ').groupby('N').mean()['c']
res_sum

	theta	ci_asy_lb	ci_asy_ub	sd	cov_asy
N
10	0.901047	0.247244	1.554849	0.433972	0.7438
20	0.946928	0.415006	1.478851	0.307562	0.8348
30	0.966928	0.508733	1.425123	0.252467	0.8758
50	0.982816	0.612700	1.352932	0.198106	0.9022
100	0.992174	0.723367	1.260981	0.141238	0.9270
200	0.995550	0.802543	1.188557	0.101163	0.9376
500	0.999888	0.876514	1.123263	0.062520	0.9468
2000	0.998711	0.936884	1.060537	0.031484	0.9524

From the first column we see that indeed the estimator appears consistent. We also notice that the asymptotic standard errors are centered around the point estimates by cosntruction. This means that they won't cover the parameter well in finite sample because of the bias in the parameter. They are also symetric, yet the distribution of the estimator might not be in finite sample either.

Finally, we can compute the coverage of the CI, the actual probability that it containes the parameter. We see that indeed it does converge in probability to 0.95, but that it does poorly in small sample.

Computing bootstrap Confidence Intervals

We are going to use the percentile bootstrap as well as the $BC_a$ bootstrap.

In particular the $BC_a$ is guaranteed to second order accurate. Meaning that its rate of convergence is one order higher than the percentile bootstrap of the asymptotic inference.

def bs_pi(X,estimator,R,bc=False):
    N = len(X)
    theta = np.zeros(R) 

    for r in range(R):        
        # redraw from X and apply estimator
        I = np.random.randint(N,size=N)
        theta[r] = estimator(X[I])

    # extract CI
    lb,ub = np.quantile(theta,[0.025,0.975])

    if bc:
        bias = np.mean(theta) - estimator(X)
        lb = lb - bias
        ub = ub - bias

    return(lb,ub)

def F_normal(N, bs=True, bias=0, bc=False):
    X = np.random.normal(size=N)
    varn = var_stat(X,bias=bias)

    # compute asymptotic standard errors
    mu  = X.mean()
    s2  = ( (X-mu)**2 ).mean() 
    mu4 = ( (X-mu)**4 ).mean() 

    ci_asy_lb = varn - 1.96*np.sqrt( (mu4 - s2**2)/N)
    ci_asy_ub = varn + 1.96*np.sqrt( (mu4 - s2**2)/N)
    ci_pi_lb, ci_pi_ub = bs_pi(X,var_stat,500,bc=bc)

    return({'theta':varn, 
                'ci_asy_lb': ci_asy_lb,
                'ci_asy_ub': ci_asy_ub,
                'ci_pi_lb': ci_pi_lb,
                'ci_pi_ub': ci_pi_ub,
                'N':N})

from tqdm import trange, tqdm, tqdm_notebook
import warnings
warnings.simplefilter('ignore')

R = 100
res = [F_normal(N,bc=False) for N in tqdm_notebook([10,20,30,50,75,100,200,500]) for _ in  tqdm_notebook(range(R),leave=False)]

# R = 500 # repeat 20 times to compute an average
# res_bs = [F_normal(N) for N in tqdm_notebook([10,20,30,50,75,100]) for _ in  tqdm_notebook(range(R),leave=False)]
# res_bs = pd.DataFrame(res_bs)

  0%|          | 0/8 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]

res = pd.DataFrame(res)
res_sum = res.groupby('N').mean()
# res_sum['lb'] = res.groupby('N')['theta'].quantile(0.025)
# res_sum['ub'] = res.groupby('N')['theta'].quantile(0.975)
#res_sum['sd'] = res.groupby('N')['theta'].std()
res_sum['cov_asy'] = res.eval('c = (ci_asy_lb < 1) &  (ci_asy_ub > 1) ').groupby('N').mean()['c']
res_sum['cov_pi'] = res.eval('c = (ci_pi_lb < 1) &  (ci_pi_ub > 1) ').groupby('N').mean()['c']
res_sum

	theta	ci_asy_lb	ci_asy_ub	ci_pi_lb	ci_pi_ub	cov_asy	cov_pi
N
10	0.922611	0.232453	1.612768	0.246309	1.524426	0.79	0.76
20	0.915490	0.391975	1.439004	0.415024	1.412330	0.85	0.84
30	0.966602	0.515642	1.417563	0.532244	1.405382	0.88	0.87
50	0.994769	0.623759	1.365779	0.636390	1.358784	0.93	0.93
75	1.000314	0.690987	1.309641	0.703829	1.310524	0.90	0.90
100	0.985057	0.715681	1.254434	0.724286	1.254821	0.94	0.92
200	1.006862	0.816019	1.197706	0.823206	1.196777	0.95	0.95
500	1.002962	0.878143	1.127781	0.882316	1.128654	0.96	0.95

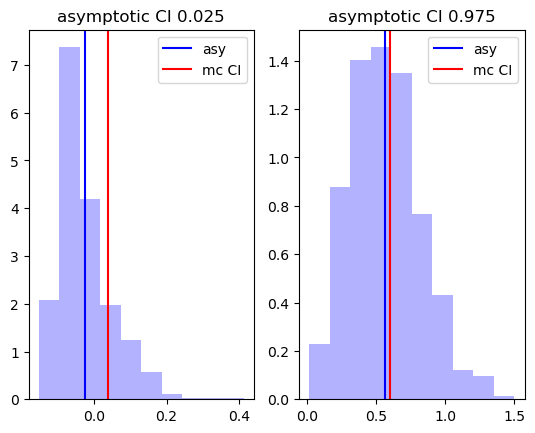
We see here that the percentile boostrap doesn't provide much of an advantage when compared to the asymptotic confidence interval. We then turn to the BCa bootstrap.

Call $\theta^*(r)$ the different bootstrap replications. The percentile boostrap simply computes the 0.025 and 0.975 quantiles in this replicated distribution.

The BCa approach, on the other hand uses adjusted quantiles. It uses:

$\alpha_1 = \Phi\Big(z_0 + \frac{z_0 + z^{(\alpha)}}{ 1-a (z_0 + z^{(\alpha)}}\Big)$$ $$\alpha_2 = \Phi\Big(z_0 + \frac{z_0 + z^{(1-\alpha)}}{ 1-a (z_0 + z^{(1-\alpha)}}\Big)$

where $z$ and $a$ are computed from the replications. For instance

$z_0= \Phi^{-1}\Big( \frac{\#[ \theta^*(r) < \theta_n ]}{R} \Big)$

the acceleration $a$ has to do with higher order moments of the distribution of replications.

Importantly, the BCa conf interval can be shown to be second order accurate. While we usually have that

$Pr[ \theta < \theta_{lb} ] \simeq 0.025 + \frac{c}{\sqrt{n}}$

For the BCa it is the case that

$Pr[ \theta < \theta_{lb} ] \simeq 0.025 + \frac{c}{n}$

np.random.seed(234453)

def F_normal(N, bs=True, bias=0):
    X  =  (1/0.6)*np.abs(np.random.normal(size=N))
    #X  =  np.random.normal(size=N)
    #X = np.random.pareto(5.0, N) # !!! new distribution here

    varn = var_stat(X,bias=bias)

    # compute asymptotic standard errors
    mu  = X.mean()
    s2  = ( (X-mu)**2 ).mean() 
    mu4 = ( (X-mu)**4 ).mean() 

    ci_asy_lb = varn - 1.96*np.sqrt( (mu4 - s2**2)/N)
    ci_asy_ub = varn + 1.96*np.sqrt( (mu4 - s2**2)/N)

    # boostrap
    ci_pi_lb, ci_pi_ub = bs_pi(X,var_stat,2000)
    bs_bca = boot.ci(X, var_stat, method="bca", n_samples=2000)

    return({'theta':varn, 
                'ci_asy_lb': ci_asy_lb,
                'ci_asy_ub': ci_asy_ub,
                'ci_pi_lb': ci_pi_lb,
                'ci_pi_ub': ci_pi_ub,
                'ci_bca_lb': bs_bca[0],
                'ci_bca_ub': bs_bca[1],
                'N':N})

R = 100 # number of sample replciations (not the number of draws in bootstrap)
res = [F_normal(N) for N in tqdm_notebook([10,20,30,50,75,100,200,500]) for _ in  tqdm_notebook(range(R),leave=False)]
#res = [F_normal(N) for N in tqdm_notebook([500]) for _ in  tqdm_notebook(range(R),leave=False)]

res = pd.DataFrame(res)

  0%|          | 0/8 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]



  0%|          | 0/100 [00:00<?, ?it/s]

res_sum = res.groupby('N').mean()
res_sum['lb'] = res.groupby('N')['theta'].quantile(0.025)
res_sum['ub'] = res.groupby('N')['theta'].quantile(0.975)
res_sum['sd'] = res.groupby('N')['theta'].std()
res_sum['cov_asy'] = res.eval('c = (ci_asy_lb < 1) &  (ci_asy_ub > 1) ').groupby('N').mean()['c']
res_sum['cov_pi'] = res.eval('c = (ci_pi_lb < 1) &  (ci_pi_ub > 1) ').groupby('N').mean()['c']
res_sum['cov_bca'] = res.eval('c = (ci_bca_lb < 1) &  (ci_bca_ub > 1) ').groupby('N').mean()['c']
#res_sum['cov_abc'] = res.eval('c = (ci_abc_lb < 1) &  (ci_abc_ub > 1) ').groupby('N').mean()['c']
res_sum

	theta	ci_asy_lb	ci_asy_ub	ci_pi_lb	ci_pi_ub	ci_bca_lb	ci_bca_ub	lb	ub	sd	cov_asy	cov_pi	cov_bca
N
10	0.869517	0.174061	1.564974	0.202859	1.453777	0.354924	1.755925	0.211509	1.918902	0.450517	0.68	0.67	0.75
20	0.900818	0.365291	1.436345	0.386892	1.405077	0.508638	1.676115	0.423087	1.625944	0.340470	0.74	0.71	0.82
30	0.987153	0.462526	1.511781	0.490699	1.501187	0.597912	1.750266	0.477577	1.742428	0.317701	0.83	0.82	0.86
50	0.987274	0.560474	1.414073	0.581286	1.413819	0.664168	1.591834	0.619902	1.417006	0.209673	0.93	0.93	0.93
75	0.996387	0.638414	1.354359	0.656981	1.359801	0.719417	1.492791	0.677484	1.392168	0.190277	0.89	0.89	0.92
100	0.994734	0.679935	1.309534	0.697178	1.316708	0.751731	1.427705	0.659599	1.400612	0.198564	0.87	0.87	0.91
200	1.025432	0.790483	1.260380	0.800097	1.266053	0.833182	1.323666	0.812848	1.273392	0.129253	0.93	0.93	0.92
500	0.988418	0.843802	1.133034	0.847192	1.135461	0.863119	1.155419	0.839146	1.121996	0.074282	0.92	0.92	0.92

We can also look at the shape of the interval

res_sum = res.groupby('N').mean()
res_sum['lb'] = res.groupby('N')['theta'].quantile(0.025)
res_sum['ub'] = res.groupby('N')['theta'].quantile(0.975)
res_sum['sd'] = res.groupby('N')['theta'].std()
res_sum['cov_asy'] = res.eval('c = (ci_asy_lb < 1) &  (ci_asy_ub > 1) ').groupby('N').mean()['c']
res_sum['cov_pi'] = res.eval('c = (ci_pi_lb < 1) &  (ci_pi_ub > 1) ').groupby('N').mean()['c']
res_sum['cov_bca'] = res.eval('c = (ci_bca_lb < 1) &  (ci_bca_ub > 1) ').groupby('N').mean()['c']
#res_sum['cov_abc'] = res.eval('c = (ci_abc_lb < 1) &  (ci_abc_ub > 1) ').groupby('N').mean()['c']
res_sum

	theta	ci_asy_lb	ci_asy_ub	ci_pi_lb	ci_pi_ub	ci_bca_lb	ci_bca_ub	lb	ub	sd	cov_asy	cov_pi	cov_bca
N
10	0.869517	0.174061	1.564974	0.202859	1.453777	0.354924	1.755925	0.211509	1.918902	0.450517	0.68	0.67	0.75
20	0.900818	0.365291	1.436345	0.386892	1.405077	0.508638	1.676115	0.423087	1.625944	0.340470	0.74	0.71	0.82
30	0.987153	0.462526	1.511781	0.490699	1.501187	0.597912	1.750266	0.477577	1.742428	0.317701	0.83	0.82	0.86
50	0.987274	0.560474	1.414073	0.581286	1.413819	0.664168	1.591834	0.619902	1.417006	0.209673	0.93	0.93	0.93
75	0.996387	0.638414	1.354359	0.656981	1.359801	0.719417	1.492791	0.677484	1.392168	0.190277	0.89	0.89	0.92
100	0.994734	0.679935	1.309534	0.697178	1.316708	0.751731	1.427705	0.659599	1.400612	0.198564	0.87	0.87	0.91
200	1.025432	0.790483	1.260380	0.800097	1.266053	0.833182	1.323666	0.812848	1.273392	0.129253	0.93	0.93	0.92
500	0.988418	0.843802	1.133034	0.847192	1.135461	0.863119	1.155419	0.839146	1.121996	0.074282	0.92	0.92	0.92

res_sum.eval("width = ub-lb").eval("width_asy = ci_asy_ub-ci_asy_lb").eval("width_bca = ci_bca_ub-ci_bca_lb")

	theta	ci_asy_lb	ci_asy_ub	ci_pi_lb	ci_pi_ub	ci_bca_lb	ci_bca_ub	lb	ub	sd	cov_asy	cov_pi	cov_bca	width	width_asy	width_bca
N
10	0.869517	0.174061	1.564974	0.202859	1.453777	0.354924	1.755925	0.211509	1.918902	0.450517	0.68	0.67	0.75	1.707393	1.390913	1.401001
20	0.900818	0.365291	1.436345	0.386892	1.405077	0.508638	1.676115	0.423087	1.625944	0.340470	0.74	0.71	0.82	1.202857	1.071054	1.167477
30	0.987153	0.462526	1.511781	0.490699	1.501187	0.597912	1.750266	0.477577	1.742428	0.317701	0.83	0.82	0.86	1.264851	1.049255	1.152354
50	0.987274	0.560474	1.414073	0.581286	1.413819	0.664168	1.591834	0.619902	1.417006	0.209673	0.93	0.93	0.93	0.797105	0.853599	0.927665
75	0.996387	0.638414	1.354359	0.656981	1.359801	0.719417	1.492791	0.677484	1.392168	0.190277	0.89	0.89	0.92	0.714684	0.715945	0.773374
100	0.994734	0.679935	1.309534	0.697178	1.316708	0.751731	1.427705	0.659599	1.400612	0.198564	0.87	0.87	0.91	0.741013	0.629599	0.675975
200	1.025432	0.790483	1.260380	0.800097	1.266053	0.833182	1.323666	0.812848	1.273392	0.129253	0.93	0.93	0.92	0.460544	0.469897	0.490484
500	0.988418	0.843802	1.133034	0.847192	1.135461	0.863119	1.155419	0.839146	1.121996	0.074282	0.92	0.92	0.92	0.282851	0.289232	0.292299

We want to think about whether the finite sample distribution is symetric around the estimates. We can first look at the dsitribution in realizeded valued.

plt.hist(res.query("N==20")['theta'],alpha=0.3)
plt.axvline(x=1.0,color="red")
plt.axvline(x=res.query("N==20")['theta'].mean())
plt.axvline(x=res.query("N==20")['theta'].quantile(0.025),linestyle=":")
plt.axvline(x=res.query("N==20")['theta'].quantile(0.975),linestyle=":")

<matplotlib.lines.Line2D at 0x7f098d168f10>

From this we see that when constructing the CI around the estimate, we might not want to use a symetric distribution. The bootstrap can help with that since it picks up the non symmetry through the replication. We can check if the bootstrap is able to reproduce such shape due to finite sample issues.

res.eval("shape_bca = (ci_bca_ub - theta)/(theta - ci_bca_lb)").groupby('N')['shape_bca'].mean()

N
10     1.756288
20     1.904075
30     1.925115
50     1.835687
75     1.742245
100    1.749908
200    1.540531
500    1.334661
Name: shape_bca, dtype: float64

res.eval("shape_bca = (ci_pi_ub - theta)/(theta - ci_pi_lb)").groupby('N')['shape_bca'].mean()

N
10     0.849145
20     0.953922
30     1.015952
50     1.038469
75     1.054027
100    1.070927
200    1.063228
500    1.041023
Name: shape_bca, dtype: float64

res.eval("shape_bca = (ci_asy_ub - theta)/(theta - ci_asy_lb)").groupby('N')['shape_bca'].mean()

N
10     1.0
20     1.0
30     1.0
50     1.0
75     1.0
100    1.0
200    1.0
500    1.0
Name: shape_bca, dtype: float64

res_sum = res.groupby('N').mean()
res_sum['lb'] = res.groupby('N')['theta'].quantile(0.025)
res_sum['ub'] = res.groupby('N')['theta'].quantile(0.975)
res_sum.eval("shape = (ub -theta)/(theta - lb)")

	theta	ci_asy_lb	ci_asy_ub	ci_pi_lb	ci_pi_ub	ci_bca_lb	ci_bca_ub	lb	ub	shape
N
10	0.869517	0.174061	1.564974	0.202859	1.453777	0.354924	1.755925	0.211509	1.918902	1.594790
20	0.900818	0.365291	1.436345	0.386892	1.405077	0.508638	1.676115	0.423087	1.625944	1.517855
30	0.987153	0.462526	1.511781	0.490699	1.501187	0.597912	1.750266	0.477577	1.742428	1.482165
50	0.987274	0.560474	1.414073	0.581286	1.413819	0.664168	1.591834	0.619902	1.417006	1.169749
75	0.996387	0.638414	1.354359	0.656981	1.359801	0.719417	1.492791	0.677484	1.392168	1.241073
100	0.994734	0.679935	1.309534	0.697178	1.316708	0.751731	1.427705	0.659599	1.400612	1.211083
200	1.025432	0.790483	1.260380	0.800097	1.266053	0.833182	1.323666	0.812848	1.273392	1.166415
500	0.988418	0.843802	1.133034	0.847192	1.135461	0.863119	1.155419	0.839146	1.121996	0.894860